More on Why Asteroid Will Miss Mars

I decided my previous post on the Mars asteroid was not clear enough.  Above is a figure from NASA's Near Earth Asteroid site  from 9 January.  The thin white line with the orange circle on it is the orbit of Mars.  The blue line is the most likely path, which corresponds to s=0 on the bell curve of the previous post.   The bunch of white dots are the possible points of closest approach given the error in the measurements (the path of the asteroid for each dot would be a line parallel to the blue line going through that dot).  

As you can see, the dots are bunched around the most probable value and taper off in either direction—in the same way that the the area under a bell curve decreases away from the center.  s, the distance from the blue line to Mars divided by the size of the error, is 3.7, giving a probability of 10,000:1.

 

Here is what the asteroid figure looked like two weeks ago:

Notice that the scale here is 500,000 km, so this is zoomed out by a factor of 5 from the 9 January picture.  Two things have happened in the fortnight.  First, the position of the blue line has changed a little.  More importantly, the size of the error was a lot bigger two weeks ago.  Back then the error was large enough so that the distance from the blue line to Mars divided by the error was only 2.2, giving a probability of 25:1.

So the probability changed from 25:1 to 10,000:1 over the last two weeks mainly because the error in the path decreased, making  s  increase (again, s is the distance from the blue line to Mars divided by the error, and it is also the position on the bell curve of the previous post).

Read More...

Summary only...

Why Asteroid Will Miss Mars

Last month, it was reported that a very small asteroid had a 1-in-75 chance of hitting Mars, which was very exciting.  It would be awesome to see the effects of such a collision.  Then the number was 1-in-25, which was even more exciting.  Now the number has dropped to 1-in-10,000, so it is very unlikely to happen.  How could the numbers change that much?

[see also next post, More on Why Asteroid Will Miss Mars]

Suppose it was your job to calculate the probability the asteroid would hit.  You would take the most accurate measurements of the asteroid, extrapolate its position, and come up with your best estimate of the path for the asteroid.  Now there would be some uncertainty in your estimate for the path.  Let's call s the distance of closest approach to Mars of your best guess for the path.  The plot of  probabilities is given by this bell curve (also called a Gaussian curve):

If you calculated that s=0, that the most likely path just grazes the surface of Mars, then all paths to the right of s=0 would hit Mars, and you'd say that the probability of hitting was 1/2 (half the area under the curve is to the right of s=0).  If you calculated that s=2.2 (which they did in December), then only paths more than 2.2 standard deviations from the most likely path would hit Mars, a chance of 75 to 1 (less than 2.1%).  And if your calculation shifted just a little, so that s=3.7 (the value now), then only the paths more than 3.7 standard deviations from the most likely path would hit Mars, a chance of 10,000 to 1.  It takes only a little shift out on a bell curve to make the probability plummet.   

And so a small refinement in measurements of the asteroid positions made the impact probability... crash.

 

[Notice that I did not put any units on s, because s is really distance/error-in-path-estimation, so that s=1 corresponds to whatever 1 standard deviation is in this case.  We don't need the actual distances in km because we are taking a ratio.]

[image from here, arrows and text added by me (feel free to use)]

[confidence: likely, my qualifications: informed]

Read More...

Summary only...

Champagne Science

Three be the things I shall never attain:

Envy, content, and sufficient champagne.  

-from Inventory by Dorothy Parker 

 

Happy New Year! First, to those of you who don't drink, sorry, this post is not for you.  Well, actually, you can pretend we are talking about seltzer, which has similar properties.

I love the taste of dry champagne, its bubbly texture, and the way it makes me smile.  I'm afraid I'm a bit spoiled when it comes to champagne -- I just don't like the cheap stuff. 

 

"Champagne" is sparkling wine made in a particular way in the Champagne region of France, which accounts for only about 3% of the French vineyard area.  No sparkling wine from outside that region can legally be called "champagne", even if it is made in exactly the same way.  Demand has increased enough of late that the French are considering expanding the official region, which would magically transmute some  "sparkling wine" into "champagne".  Who says there is no alchemy?  Seriously, a designation should depend upon the quality of a product, not where it was produced.  But perhaps the quality is better.  A wine expert I know writes:

"The chard and pinot noir grapes surely do taste differently when grown in Champagne, because of temperature and soil, and the acidity developed there makes champagne taste like champagne. So, while I think it reasonable that the territory be expanded to next door, where perhaps the hundreds of years old techniques, quality of soil, and climate are similar, it can in no way be expanded to Italy or Germany. The sparkling wine from those or any other countries might be great,but they just wouldn't be champagne."

Everything below applies equally to all sparkling wine, regardless of its geographic origin.

Let us take a brief break from appreciating the tingling taste of the effervescent bubbles, and ask what science has to say about champagne.    I want to mention two aspects: the established physics of the bubbles, and the recent results on bubble trains.  It is the latter which sets the "confidence level" for this post at likely instead of established (see bottom note and original reference to these notes). 

 

Sparkling wine sparkles because of dissolved carbon dioxide (CO2) in the wine, which is mostly water.  It is not uncommon for some gas to be dissolved in water (oxygen, O2,  dissolved in water is what fish breathe), but there is far more CO2 in champagne than would be found naturally.   The pressure of the sealed bottle keeps bubbles from forming in the same way that someone stepping on a balloon would keep you from blowing it up.   When you remove the cork, it's like the person stepping off the balloon -- bubbles can form with abandon.  Unlike many solids which dissolve in water, like sugar or salt, the amount of CO2 you can dissolve goes down as the water temperature rises, which is why it is good to keep champagne chilled.

There has been some recent work in understanding how the bubbles form and why they form patterns of bubbles in trains.  When you uncork sparkling wine, it becomes a supersaturated solution -- there is more CO2 in the wine than can be held there at that temperature and pressure.  But it can't all come out at once, unless you are silly enough to shake the bottle, because bubbles need something to nucleate (begin) on.  When you shake the bottle, you form all sorts of bubbles which can quickly grow bigger and suck out all the CO2.  So how do bubbles form if you are gentle with your champagne?  Well, recent research (e.g., this and this) says that little pieces of dust or lint on the glass allows one bubble after another to nucleate, forming different patterns of bubble trains depending on the pressure, temperature and how flat the champagne is.

 

Enough!  Don't let the bubbly get too flat before you make your toast!   Happy New Year!

[picture from artlebedev]

[confidence level: likely, my qualifications: informed]

Read More...

Summary only...

Thought Experiment: Orbiting Cannonballs

A baby puts everything in its mouth because its mouth is one of its most effective sensory organs.   For adults, "seeing is believing", because we (or at least those of us who are sighted) get most of our information via our eyes.  But what do we do when we want to observe something beyond our experience—something not accessible to the five external senses?  We imagine, of course.  But when that imagination is tempered by logic and care, it really becomes an eye on an internal world.

Physicists call it the Thought Experiment. Actually, since it was popularized by Albert Einstein, whose native tongue was German, it is usually referred to by its German name Gedankenexperiment, which literally translated is ..."thought experiment".

  [Aside: I love the song "Die Gedanken Sind Frei", which I learned of from the Unitarian Universalist hymnal.]

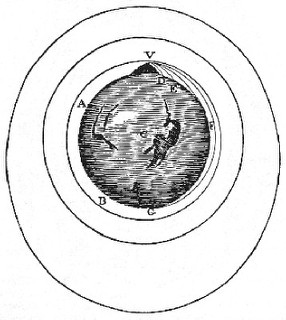
This diagram is due to one the most influential scientists in history, Sir Isaac Newton.  (More about him and my little intersection with him later.)  It is a diagram designed to explain how objects can be put into orbit.  It was drawn more than 250 years before Sputnik, and nearly 100 years before the first balloon flight.  It is still, in my opinion, the clearest way of explaining how satellites orbit.

A cannon sits atop a mountain, which by the looks of it is around 500 miles tall, which is about 100 times the height of Mt. Everest.  It shoots cannonballs that fall back to the Earth in the usual parabolic path.  Each successive cannonball is shot faster so that it goes farther than the last.  Eventually, when a cannonball's trajectory curves more slowly than the orb of Earth, it falls forever without running into the Earth.  In other words, it goes into orbit around the Earth.

 

The only way Newton could "see" this was in his mind.  This thought experiment allowed Newton to extrapolate from the world of his everyday sense to things on the scale of the Earth or even the solar system.  With this simple diagram, he showed how things orbit.  The moon orbits the Earth because it falls, due to gravity, in a gentle curve around and around the Earth.

But it is important to look at a diagram like this with care.  It is not enough to glance with your inner eye.  You have to look carefully.  Confession: When I looked at the diagram, I assumed that by fine tuning the speed of the cannonball, you could get it to hit anywhere around the Earth, say where the A or the B are.  But they are not potential landing sites.  I should have thought about it more.  Then I came across this Java applet which lets  you simulate the trajectory for any speed you wish.  I soon realized that once the cannonball is fast enough to make it past the South pole, G, it would make it all the way around.  You can't get it to hit near A or B (neglecting friction).   Try it.   Find the largest speed for which the cannonball still hits the Earth.  Then see what happens 1 mile/hr more than that.  Like many other physical situations, there is a symmetry that can tell you what is going on.  If the cannonball can make to the South Pole, then it traces a path on the other side of the Earth that is a mirror image of the path it took getting there, and hits the cannon from behind.  The whole path is an ellipse with the closest point at the South Pole.

 

[confidence level: established, my qualifications: trained]

Read More...

Summary only...